Matrix Chain Multiplication
Problem Statement:
find the minimum number of multiplications needed to multiply \(A_1, A_2, A_3, ...A_n\) where \(A_i\) is a matrix .
since number of columns in \(A_{i-1}\) is same as number of rows in \(A_{i}\) the input to this problem is an array \(order[\ ]\) of n+1 numbers where first number is number of rows in \(A_1\) and \(i^{th}\) (i > 1) number is number of colums in \(A_{i}\). Finally order of matrix \(A_{i}\) is \(order[i-1] \times order[i]\) .
Algorithm
1. slipt the matrix multiplication \(A_i.A_{i+1}....A_j\) for every k from i to j.
2. We call mcm( ) for matrices \(A_i\) to \(A_k\) and for \(A_{k+1}\) to \(A_j\) and add these two with \(order[i - 1] * order[k] * order[j]\) which is number of multiplication needed for multiplying these two parts.
3. return minimum value of \(mcm(A_i ...A_k) + mcm(A_{k+1} .. A_j) + order[i - 1] * order[k] * order[j]\) for all k in i to j
4. The same thing can be illustrated by the following figure.
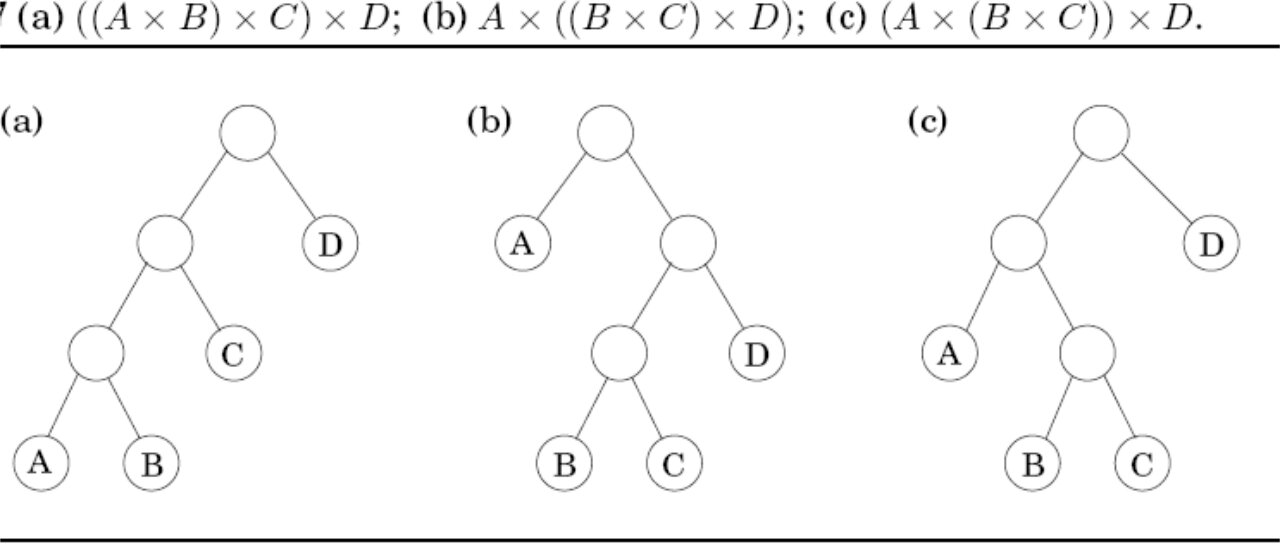
Code :
// matrix chain multiplication
#include <bits/stdc++.h>
using namespace std;
int mcm(int order[], int i, int j)
{
if (i == j)
{
return 0;
}
int min = INT_MAX;
for (int k = i; k < j; k++)
{
int count = mcm(order, i, k) + mcm(order, k + 1, j) + order[i - 1] * order[k] * order[j];
if (count < min)
{
min = count;
}
}
return min;
}
int main()
{
int n;
cin >> n;
int order[n];
for (int i = 0; i < n; i++)
{
cin >> order[i];
}
cout<<" min multiplications = "<<mcm(order,1,n-1)<<"\n";
}
Complexity Analysis :
Time complexity : \(O(n^3)\)